Attention

This website is still under construction.

Enigma 001 : The Treasure Door

The adventure starts here! Alice is walking on a distant planet. Suddenly, she comes across two guardians, two doors and a treasure. Will she be able to answer the riddle correctly to win the key to the treasure? A classic problem that can be translated on a quantum computer. It’s a nice way to make the leap into quantum programming and apply the concepts of state superposition, entanglement and quantum parallelism.

Make sure to watch the following video before getting started with these exercises:

Important

On this website, you will be able to write and run your own Python code. To do so, you will need to click on the “Activate” button to enable all the code editors and establish a connection to a Kernel. Once clicked, you will see that the Status widget will start to show the connection progress, as well as the connection information. You are ready to write and run your code once you see Status:Kernel Connected and kernel thebe.ipynb status changed to ready[idle] just below. Please note that that refreshing the page in any way will cause you to lose all the code that you wrote. If you run into any issues, please try to reconnect by clicking on the “Activate” button again or reloading the page.

Note

When running your code, you’ll know that the code is running if you see kernel thebe.ipynb status changed to ready[busy]. If it seems to stay on ready[idle] when running your code and/or you’re not getting an output when you’re supposed to, it most likely means that there’s an error in your code. Since the code editor seems to be struggling with outputting error messages, there is no output.

Run the cell below to install the necessary packages.

import sys
!{sys.executable} -m pip install qiskit==1.1.1
!{sys.executable} -m pip install qiskit_aer==0.14.2
!{sys.executable} -m pip install pylatexenc==2.10

# Import necessary modules
import numpy as np
from qiskit import QuantumCircuit

Exercise 1 - Code writing

×

Sometimes a quantum circuit can be simplified. One way of achieving this is by cancelling some quantum gates. Could you simplify the following circuit?

problem_qc = QuantumCircuit(3)

problem_qc.h(0)
problem_qc.h(2)
problem_qc.cx(0, 1)
problem_qc.barrier(0, 1, 2)
problem_qc.cx(2, 1)
problem_qc.x(2)
problem_qc.cx(2, 0)
problem_qc.x(2)
problem_qc.barrier(0, 1, 2)
problem_qc.swap(0, 1)
problem_qc.x(1)
problem_qc.cx(2, 1)
problem_qc.x(0)
problem_qc.x(2)
problem_qc.cx(2, 0)
problem_qc.x(2)

problem_qc.draw()

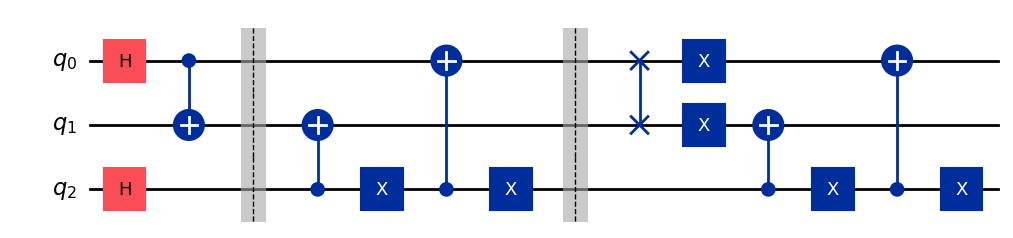
Try simplifying the circuit and rerun the calculation between each simplification to make sure you always get the same histogram. You can compare your answer to the solution.

problem_qc = QuantumCircuit(12)

### Start writing your code here. ###


# Visualize the circuit
problem_qc.draw('mpl')

Click to reveal HINT 1

The NOT, CNOT, and Hadamard gates are their own inverse. That means that if two of these gates are placed side by side they can simply be taken off.

Click to reveal HINT 2

The SWAP gate can be taken off if the subsequent operations are adjusted between the two qubits.

Click to reveal HINT 3

If a CNOT has the same control and target as another CNOT for which two NOT gates are applied before and after the control qubit, this can be simplified to a single NOT gate on the target qubit of the CNOT as a NOT gate is applied to the target whether the control qubit is initially in state 0 or 1.

Click to reveal HINT 4

The circuit can be simplified until only three gates remain in the algorithm.

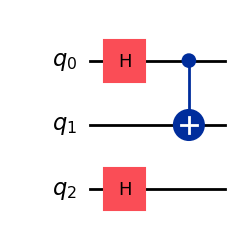
Click to reveal the answer

problem_qc = QuantumCircuit(3)
problem_qc.h(0)
problem_qc.cx(0,1)
problem_qc.h(2)

# Visualize the circuit
problem_qc.draw('mpl')

Exercise 2 - Quick quiz

Can you interpret the results of Question 1?

Submit Answer

Exercise 3 - Quick quiz

Launching algorithms on modern quantum computers does not always lead to 100% successful results, as some noise sometime causes bad results. If you launch the whole circuit on a real quantum computer, multiple times, what percentage of good answers might you get?

Submit Answer